Probabilidad condicionada es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribe P(A|B), y se lee «la probabilidad de A dado B.
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no dependiendo de la interpretación que se le dé a los eventos.
El condicionamiento de probabilidades puede lograrse aplicando el teorema de Bayes.
Definición
Dado un espacio de probabilidad  y dos eventos (o sucesos)
y dos eventos (o sucesos) 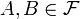 con P(B) > 0, la probabilidad condicional de A dado B está definida como:
con P(B) > 0, la probabilidad condicional de A dado B está definida como:
 y dos eventos (o sucesos)
y dos eventos (o sucesos) 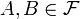 con P(B) > 0, la probabilidad condicional de A dado B está definida como:
con P(B) > 0, la probabilidad condicional de A dado B está definida como:Interpretación
 se puede interpretar como, tomando los mundos en los que B se cumple, la fracción en los que también se cumple A. Si el evento B es, por ejemplo, tener la gripe, y el evento A es tener dolor de cabeza,
se puede interpretar como, tomando los mundos en los que B se cumple, la fracción en los que también se cumple A. Si el evento B es, por ejemplo, tener la gripe, y el evento A es tener dolor de cabeza,  sería la probabilidad de tener dolor de cabeza cuando se está enfermo de gripe.
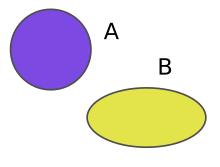
sería la probabilidad de tener dolor de cabeza cuando se está enfermo de gripe.Gráficamente, si se interpreta el espacio de la ilustración como el espacio de todos los mundos posibles, A serían los mundos en los que se tiene dolor de cabeza y B el espacio en el que se tiene gripe. La zona verde de la intersección representaría los mundos en los que se tiene gripe y dolor de cabeza  . En este caso
. En este caso  , es decir, la probabilidad de que alguien tenga dolor de cabeza sabiendo que tiene gripe, sería la proporción de mundos con gripe y dolor de cabeza (color verde) de todos los mundos con gripe: El área verde dividida por el área de B. Como el área verde representa
, es decir, la probabilidad de que alguien tenga dolor de cabeza sabiendo que tiene gripe, sería la proporción de mundos con gripe y dolor de cabeza (color verde) de todos los mundos con gripe: El área verde dividida por el área de B. Como el área verde representa  y el área de B representa a P(B), formalmente se tiene que:
y el área de B representa a P(B), formalmente se tiene que:
 . En este caso
. En este caso  , es decir, la probabilidad de que alguien tenga dolor de cabeza sabiendo que tiene gripe, sería la proporción de mundos con gripe y dolor de cabeza (color verde) de todos los mundos con gripe: El área verde dividida por el área de B. Como el área verde representa
, es decir, la probabilidad de que alguien tenga dolor de cabeza sabiendo que tiene gripe, sería la proporción de mundos con gripe y dolor de cabeza (color verde) de todos los mundos con gripe: El área verde dividida por el área de B. Como el área verde representa  y el área de B representa a P(B), formalmente se tiene que:
y el área de B representa a P(B), formalmente se tiene que:Propiedades
Pero NO es cierto que

Independencia de sucesos
Dos sucesos aleatorios A y B son independientes si y sólo si:
O sea que si A y B son independientes, su probabilidad conjunta,  ó P(A,B).
ó P(A,B).
 ó P(A,B).
ó P(A,B).puede ser expresada como el producto de las probabilidades individuales. Equivalentemente:
En otras palabras, si A y B son independientes, la probabilidad condicional de A dado B es simplemente la probabilidad de A y viceversa.
Exclusividad mutua
Dos sucesos A y B son mutuamente excluyentes si y sólo si  . Entonces,
. Entonces,  .
.
 . Entonces,
. Entonces,  .
.Además, si P(B) > 0 entonces  es igual a 0.
es igual a 0.
 es igual a 0.
es igual a 0.La falacia de la probabilidad condicional
La falacia de la probabilidad condicional se basa en asumir que P(A|B) es casi igual a P(B|A). El matemático John Allen Paulos analiza en su libro El hombre anumérico este error muy común cometido por doctores, abogados y otras personas que desconocen la probabilidad.
La verdadera relación entre P(A|B) y P(B|A) es la siguiente:
Problemas de ejemplo
---La paradoja del falso positivo---
La magnitud de este problema es la mejor entendida en términos de probabilidades condicionales.
Supongamos un grupo de personas de las que el 1 % sufre una cierta enfermedad, y el resto está bien. Escogiendo un individuo al azar:
P(enfermo) = 1% = 0.01 y P(sano) = 99% = 0.99
Supongamos que aplicando una prueba a una persona que no tiene la enfermedad, hay una posibilidad del 1 % de conseguir un falso positivo, esto es:
P(positivo | sano) = 1% y P(negativo | sano) = 99%
Finalmente, supongamos que aplicando la prueba a una persona que tiene la enfermedad, hay una posibilidad del 1 % de un falso negativo, esto es:
P(negativo | enfermo) = 1% y P(positivo | enfermo) = 99%
Ahora, uno puede calcular lo siguiente:
La fracción de individuos en el grupo que están sanos y dan negativo:

La fracción de individuos en el grupo que están enfermos y dan positivo:
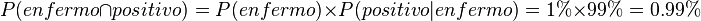
La fracción de individuos en el grupo que dan falso positivo:

La fracción de individuos en el grupo que dan falso negativo:
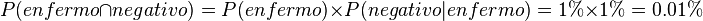
Además, la fracción de individuos en el grupo que dan positivo:

Finalmente, la probabilidad de que un individuo realmente tenga la enfermedad, dado un resultado de la prueba positivo:

En este ejemplo, debería ser fácil ver la diferencia entre las probabilidades condicionadas P (positivo | enfermo) (que es del 99 %) y P (enfermo | positivo) (que es del 50 %): la primera es la probabilidad de que un individuo enfermo dé positivo en la prueba; la segunda es la probabilidad de que un individuo que da positivo en la prueba tenga realmente la enfermedad. Con los números escogidos aquí, este último resultado probablemente sería considerado inaceptable: la mitad de la gente que da positivo en realidad está sana.
La probabilidad de tener una enfermedad rara es de 0,001: P(enfermo) = 0,001
La probabilidad de que cuando el paciente está enfermo se acierte en el diagnóstico es de 0,99: P(positivo | enfermo) = 0,99
La probabilidad de falso positivo es de 0,05: P(positivo | sano) = 0,05
Pregunta: Me dicen que he dado positivo, ¿Qué probabilidad hay de que tenga la enfermedad?









 (
(







